NORSEX algorithm

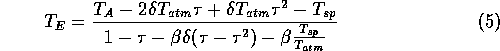
  The NORSEX algorithm is proposed by [Svendsen et al., 1983]. The algorithm estimates an effective emissivity at the surface through a linear transformation:

where 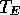is the effective brightness temperature at the surface, 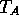is the antenna temperature, 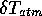is the weighted average atmospheric temperature, is the total atmospheric opacity, 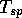is the temperature from free space and 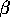is a constant close to unity. is a function of frequency, but not of polarization.

By measuring the antenna temperature in two different channels (37V and 19V), equations 2 and 3 can be used to calculate 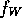, 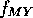and 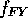. The calculated results are:

where

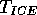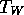and where is the physical temperature of ice, is the physical temperature of water and 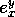is the emissivity of surface type x in channel y.

When the satellite measured tie-points are transformed through the atmosphere model given by equation 5, some observations apply. By looking careful at equations 6 through 8 it is seen, that all products are formed by a difference between the 2 terms. Each term includes the atmosphere correction at the same frequency, and therefore the constant added to 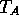in the nominator of equation 5 will have no effect. Further, since all products are formed by factors at 37GHz and 19GHz, the denominator in equation 5 appears in both the nominator and denominator in equations 6 and 7. Therefore it can be reduced, and equations 6 and 7 will produce the same results weather all or none of the measured brightness temperatures are transformed through the atmosphere.
The approach taken is to transform all brightness temperatures.