Algorithm sensitivity to physical temperature

This section will investigate, how sensitive the algorithms are to changing physical temperature of the ice. The simple linear equation between physical temperature and brightness temperature is given by

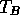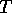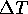where is the brightness temperature, is the emissivity and is the physical temperature. Assuming that the emissivity is independent on temperature, a change in physical ice temperature of corresponds to a change in brightness temperature of

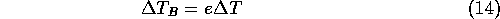
where 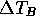is the change in brightness temperature. In real, the emissivity is dependent on temperature, and only for small temperature variations is the assumption valid. The chosen ice temperature variations, which is in good agreement with typical variations, are 5K. Because the emissivity is dependent on ice type, the change in brightness temperatures can't be modeled before the ice type is determined. The modeling has been performed in each of the 7 areas, where the mean brightness temperature in each channel has been calculated. The brightness temperature of water is assumed constant because of the thermal equilibrium between ice and water. By employing the calculated ice conditions from ice concentration section and multi-year ice fraction section, the change in brightness temperature has been determined from:

where I is the channel identifier. The physical ice temperature is modeled in a 5K interval. Equation 15 gives the change in brightness temperature in each channel, and by adding this to the calculated mean brightness temperatures in the respective areas, the impact of changing ice temperature can be found. In the 5K interval, the change in total ice concentration has been observed perfectly linear with the temperature change. Therefore a linear regression has been performed in order to find the proportionality constant. The obtained results are shown in Table 6.

  
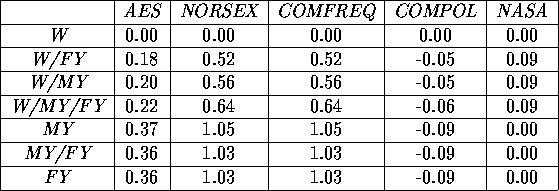
Table 6 Proportionality constant in the linear regression of the sensitivity to changing physical temperatures in the total ice concentration (in %/K)

It shows, that in all cases, except the for the NASA algorithm, the sensitivity increases with ice concentration. This is because of the constant brightness temperature of open water, where the bigger the water content, the smaller the influence of the changing ice temperature. It is seen, that the NASA algorithm is insensitive to changing physical temperatures in areas with a total ice cover. It uses the GR and PR ratios, and this gives the insensitivity to ice temperature over consolidated ice. However, in partly ice covered areas, the algorithm is influenced by changing ice temperatures (see also [Pedersen., 1991, p. 49]). The COMPOL algorithm is seen to be less sensitive than the remaining three algorithms. The largest sensitivity is in the NORSEX/COMFREQ algorithms, where the sensitivity in certain areas is about 1%/K.
In the two-channel algorithms, a change in physical temperature can be visualized in a retrieval triangle (see e.g. Figure 3 ). From a certain point in the diagram, a change in physical temperature corresponds to a change in brightness temperature along a straight line with a slope given by the emissivity in the two channels. If this line is parallel to e.g. the lines of constant ice concentration, the algorithm is insensitive to physical temperature with respect to ice concentration. From Figure 3 it can be seen, that the lines of constant ice concentration and constant multi-year ice fraction are not parallel, and therefore no two-channel algorithm can be insensitive with respect to both ice concentration and multi-year ice fraction. According to [Pedersen., 1991, p. 99-101], the size of the retrieval triangle is related to the sensitivity to measurement noise, but this also applies other noise factors. Therefore, in a big retrieval triangle, the sensitivity to changes in physical temperature is less than in a smaller triangle.
The NORSEX/COMFREQ algorithms uses the 37V and 19V channels, where the distances between the open water tie-point and the first-year/multi-year tiepoints are smaller than in the 37H and 19H channels. This can explain the rather large sensitivity in these algorithms compared to the AES algorithm. The AES algorithm uses the 19H channel, which has a low brightness temperature from open water, so the distance between the tiepoints are bigger in the 19H channel than e.g. in 37H channel that the COMPOL algorithm uses. Anyway, the COMPOL algorithm gives less sensitivity to changing ice temperatures. This can be explained by the slope of the 100% ice line, which is very close to the slope of the straight line given by the emissivities. This is not the case in the AES algorithm.

The linear regression has also been performed on the multi-year ice fraction, and the results are given in Table 7.

  
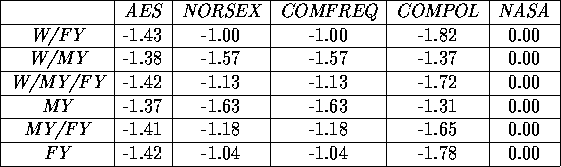
Table 7 Proportionality constant in the linear regression of the sensitivity of changing physical temperatures in the multi-year ice fraction (in %/K)

Here, the NASA algorithm is total insensitive to changing physical temperatures. The COMPOL estimation of the multi-year ice fraction is just as sensitive to changing temperatures as the remaining three algorithms. The largest sensitivity is almost 2%/K. In this case, there is no general relation between ice concentration and the order of sensitivity, but the amount of multi-year ice is seen to matter. The AES and COMPOL algorithms are seen to perform best in areas with a high multi-year ice content, while the NORSEX and COMFREQ algorithms performs best with little multi-year ice. The reason for this is probably caused by a complex connection between the slope of the constant multi-year ice lines at different positions in the retrieval triangle and the slope given by the emissivities.